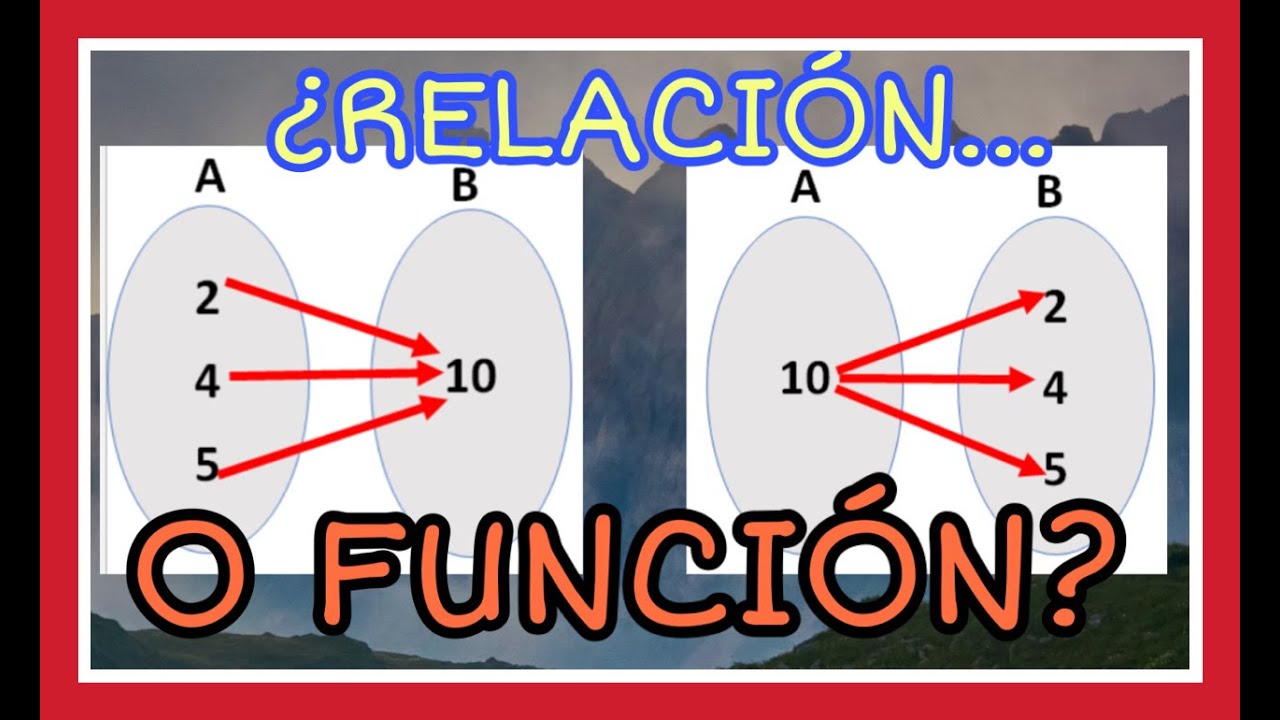
La importancia de entender la diferencia entre funciones y relaciones
En el campo de las matemáticas, las funciones y las relaciones son conceptos fundamentales que debemos comprender correctamente. Aunque a simple vista pueden parecer similares, entender su diferencia es esencial para poder aplicarlos de manera adecuada en diversos contextos. En este artículo exploraremos las características de las funciones y las relaciones, destacando sus diferencias y por qué es tan importante tener claridad al respecto.
¿Qué es una función?
Una función es una relación en la que a cada elemento de un conjunto llamado dominio le corresponde un único elemento de otro conjunto llamado rango. En otras palabras, una función establece una correspondencia exacta entre los elementos del dominio y los del rango, asegurando que no haya duplicados. Cada elemento del dominio tiene solamente una imagen en el rango.
¿Qué es una relación?
Por otro lado, una relación es un conjunto de pares ordenados que vincula elementos de dos conjuntos diferentes, conocidos como el conjunto inicial o dominio, y el conjunto final o rango. A diferencia de las funciones, en una relación un elemento del dominio puede tener más de una imagen en el rango. Esto significa que puede haber duplicados en la relación.
La diferencia clave
La diferencia clave entre funciones y relaciones radica en la unicidad de las imágenes de los elementos del dominio. En una función, cada elemento del dominio tiene una y solo una imagen en el rango. Esto garantiza que no haya ambigüedad en la asignación de valores y permite trabajar de manera precisa y determinista. En cambio, en una relación pueden existir múltiples imágenes para un mismo elemento del dominio, lo cual puede generar cierta ambigüedad o falta de determinismo en su interpretación.
Aplicaciones prácticas de las funciones y las relaciones
Las funciones son ampliamente utilizadas en diferentes áreas del conocimiento, como la física, la economía, la informática y la estadística. Su unicidad garantiza la coherencia en los cálculos y permite modelar fenómenos de manera precisa. Por ejemplo, en física, las funciones son utilizadas para describir las relaciones entre las variables en una fórmula matemática.
Por otro lado, las relaciones encuentran aplicación en contextos más flexibles donde no es necesario que haya una correspondencia única. Por ejemplo, en el ámbito de las redes sociales, las relaciones entre los usuarios pueden ser representadas mediante grafos donde los nodos corresponden a los usuarios y las aristas representan las conexiones entre ellos.
En resumen, las funciones y las relaciones son conceptos fundamentales en matemáticas que debemos entender correctamente. Una función establece una correspondencia única entre los elementos del dominio y rango, mientras que una relación permite múltiples imágenes para un mismo elemento del dominio. Comprender estas diferencias es crucial para un uso adecuado de estos conceptos en diferentes aplicaciones.
¿Puede una función tener elementos repetidos en el rango?
No, una función no puede tener elementos repetidos en el rango. Cada elemento del dominio debe tener una única imagen en el rango.
¿Qué sucede si un elemento del dominio no tiene una imagen en el rango?
Si un elemento del dominio no tiene una imagen en el rango, se considera que la función está parcialmente definida y no es válida en ese punto. En matemáticas, se dice que la función no está definida para ese valor específico.
¿Se pueden aplicar funciones y relaciones en conjunto?
Sí, es posible utilizar funciones y relaciones en conjunto en algunos casos. Por ejemplo, una relación puede estar compuesta por varios pares ordenados que a su vez pueden ser funciones individuales.
¿Cómo puedo determinar si una relación es una función o no?
Para determinar si una relación es una función, debes revisar que cada elemento del dominio tenga una única imagen en el rango. Si encuentras algún duplicado en las imágenes, entonces la relación no es una función.